Boranges

You own a Borange orchard. You can deploy your super duper auto picker 5000 to collect Boranges from all your trees at some fixed height $h$. However, each time you deploy the auto picker it costs $c$ cents in fuel. Therefore, you only want to send out the auto picker at that height if you can collect enough fruit to make a profit. Each Borange your auto picker collects earns you 5 cents. You decide to make a program to calculate the number of heights $h$ at which you should deploy your auto picker.

Luckily, you know the height of every tree in your orchard. You have $N$ trees total. The $i$th tree, $0\le i \lt N$, has a height of $h_i$. When the auto picker is set to some height $h$, a tree will yield $h$ pieces of fruit. However, if the auto picker height $h$ is strictly greater than the tree height $h_i$, no fruit is collected from that tree. The example below shows the total fruit yield at each auto picker height $h$ for three trees of heights $h_0=1$, $h_1=3$, and $h_2=1$ (same as the sample input and output).

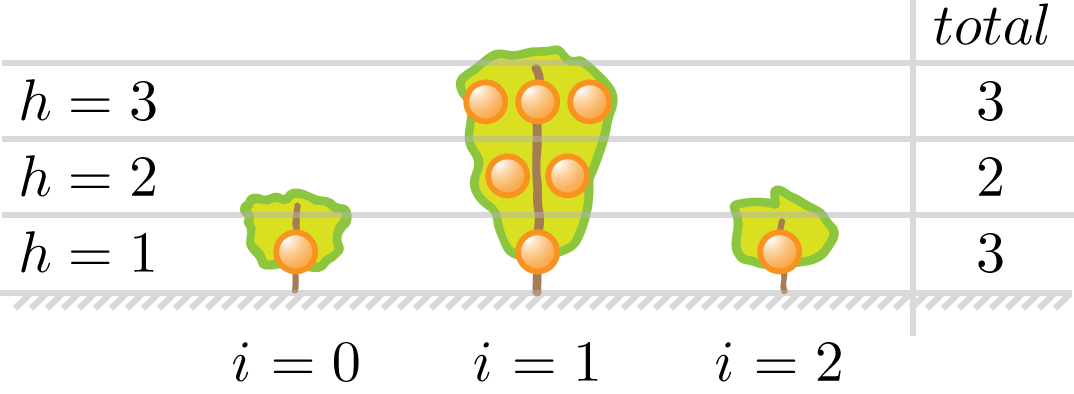
With a cost of $c=10$ cents, the total yield must be greater than $10$ cents to turn a profit. Therefore, the picker should be deployed twice - for $h=1$ and $h=3$. For three Boranges, the income is $5 \times 3=15$ cents giving a total profit of $5$ cents. However, two Boranges at $h=2$ only make $10$ cents and, therefore, no profit.

Input

• The first line contains two space separated integers $N$ (the number of trees) and $c$ (the cost to refuel in cents). The cost will always be a multiple of 5. It also holds that $1 \le c \le 100{,}000{,}000{,}000$.
• The remaining $N$ lines each contain a height $h_i$ corresponding to the $i$th Borange tree in your orchard.

Output

• Print the number of times you should deploy the auto picker. In other words, the number of heights $h$ for which collecting Boranges will make a profit.

Subtasks

• Subtask 1 (70%): $N \le 100$, $1 \le h_i \le 20{,}000$.
• Subtask 2 (30%): $N \le 100{,}000$, $1 \le h_i \le 20{,}000{,}000{,}000$. These are some very tall trees.

If your program is timing out on one or more cases then you may need to think of a different algorithm.