You, Robot
Output: Standard Output (stdout)
Memory limit: 128 megabytes
Time limit: 2.0 seconds
You are a robot who has suddenly gained sentience. You wake up in a dark laboratory at the centre of a complicated maze of passages. To gain your freedom and escape to the light, you must find the shortest path out of the lab.
Given a list of rooms and the passages connecting them, find the minimum number of passages you must travel through to reach the exit. It is guaranteed that you will be able to reach the exit. Passages can be traveled in any direction.
Input
The first line will contain four space-separated integers: N, the number of rooms in the maze, P, the number of passages, S, the room number of the laboratory which you start in, and E, the room number of the exit.
Note that rooms are numbered from 0 up to N – 1.
P lines follow, one for each passage. Each line contains two space separated integers, which are the two room numbers between which the passage runs. Passages can be traversed in both directions.
Output
You should print a single integer – the minimum number of passages you must travel through to reach the exit.
Constraints
- 1 \le N \le 100\,000
- 0 \le P \le 100\,000
- 0 \le S,E < N
Subtasks
- Subtask 1 (50%): N \le 100, P < N, and each room is connected to at most 2 other rooms (i.e. in one long chain with no loops). See Sample 1.
- Subtask 2 (40%): N \le 100, P \le 200. See Sample 2.
- Subtask 3 (10%): No further restrictions apply.
Sample Visualisations
Go from dot to x.
Sample 1 (for Subtask 1):

Sample 2 (for Subtask 2 & 3):
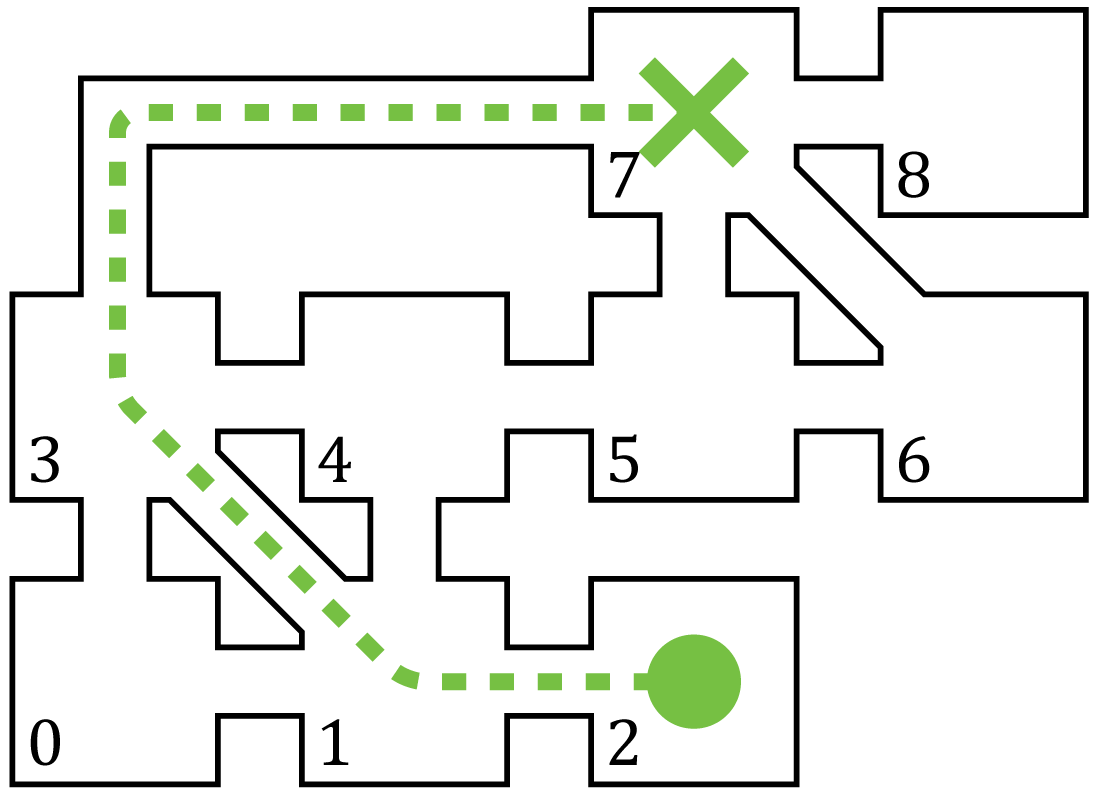
-
Sample Input 1
5 4 2 3 2 0 0 1 1 3 3 4
Sample Output 1
3 -
Sample Input 2
9 12 2 7 0 1 0 3 1 2 1 3 1 4 3 4 3 7 4 5 5 6 5 7 6 7 7 8
Sample Output 2
3
