Roller Coaster Magnate

Time are tough. Due to the pandemic NZOI has not been able to hold a residential camp, and can no longer profit off selling branded rubber ducks to a captive audience. To find a new revenue stream, Margot has decided to open a new theme park, C World$^{TM}$.

At the center of your attraction is a S.T.E.V.E. Corporation Super Roller Coaster 2000$^{TM}$. The roller coaster is made up of $N$ meter-long sections. A ride starts at the first section with an arbitrary non-negative speed, which you can control. Each following section is either an 'up' section or a 'down' section, which will decrease or increase the speed of the ride by $s$ m/s. Entering an 'up' section always decreases the ride's speed and entering a 'down' section always increases the ride's speed. If the speed of a ride reaches $0$ m/s then it will stop immediately and not continue onto further sections. The ride's brake system will stop it if it reaches the end of the last section, or attains a negative speed. Additionally, you have control of the brake system so you can decide to terminate the ride at any particular point, at which point the ejector seats will fire.

There are $M$ people in your ride. Unfortunately, because you've been cutting costs by selling dubiously hygienic watermelons, some passengers may have rather unstable stomachs due to mild food poisoning. The $i$-th person to get onto the ride is able to withstand a maximum speed of $x_i$ m/s before they throw up. You have enough money left in your budget to bribe $K$ people so that they will not leave negative reviews on the review website Kelp$^{TM}$. Therefore, you are not allowed to have more than $K$ people throw up, as negative publicity will inevitably lead to health and safety investigations.

Your task is to find the maximum distance (in meters) your ride can travel with at most $K$ people throwing up in any single section, including at the initial speed. As you can simply terminate the ride after this maximum distance, it does not matter if people would throw up past this point

Input Format

The first line of input will contain the three space-separated integers $N$, $M$ and $K$.

Following will be $N$ lines. The $i$-th such line will contain an integer $s_i$, where $s_i$ is the change in speed of the $i$-th section. Thus, for an up section $s_i \le 0$, and for a down section $s_i \ge 0$.

Finally will be $M$ lines. The $i$-th such line will contain an integer $x_i$, where $x_i$ is the maximum speed the $i$-th person can withstand without throwing up.

Output Format

Output a single integer $A (A \le N)$, where $A$ is the maximum distance (in meters) your ride can travel with at most $K$ people throwing up.

Constraints

• $1 \le N \le 100,000$
• $1 \le M \le 100,000$
• $0 \le K \le M$
• $-1000 \le s_i \le 1000$
• $0 \le x_i \le 1,000,000,000$

Subtasks

• Subtask 1 (20%): $s_i>0$ for all $i$ - that is, all sections are down sections
• Subtask 2 (20%): $N, M \le 1000$
• Subtask 3 (60%): No further constraints apply

Explanation of Sample Cases

Sample Input 1:

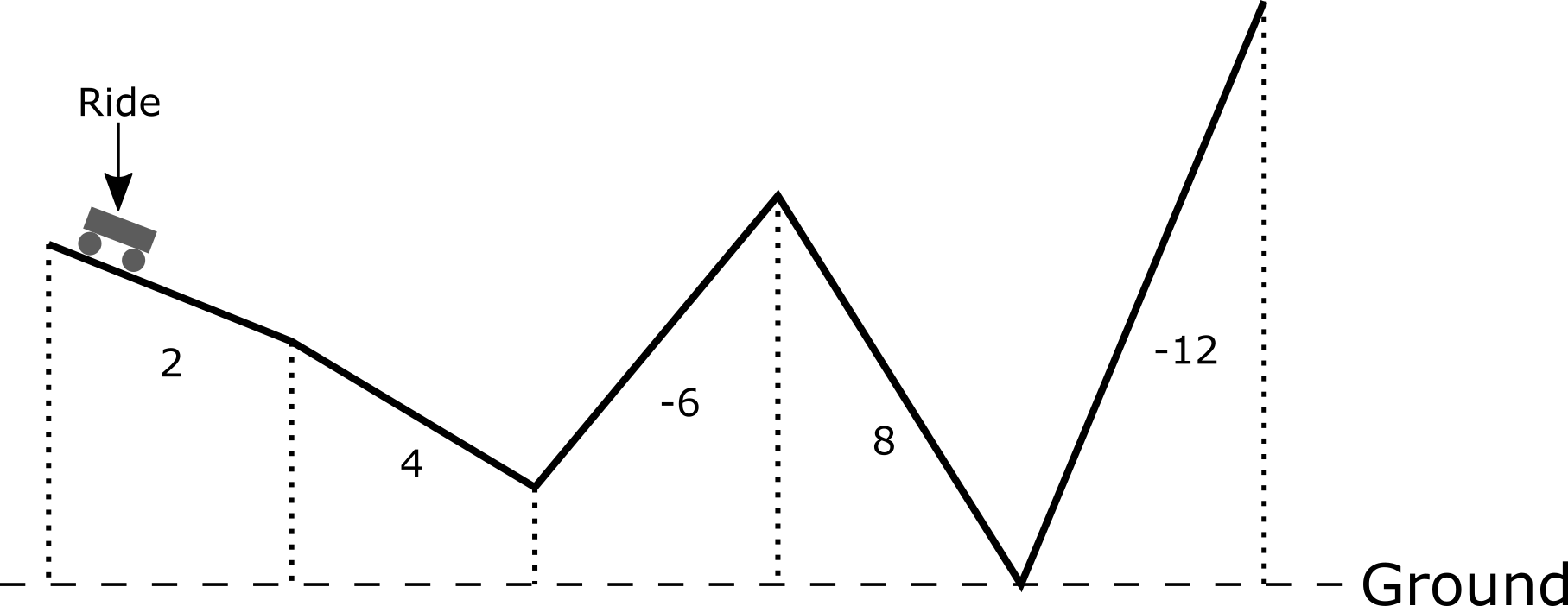
One optimal solution is to start the ride off with a speed of 2 m/s. Thus in the first section the ride has a speed of 4 m/s, increasing to 8 m/s in the next section. At this point, the first two passengers throw up as they can only stand speeds of 4 and 5 m/s respectively. In the third section the speed decreases to 2 m/s then increases to 10 m/s in the fourth section. The ride stops in the fifth section as its speed becomes negative (-2 m/s). Thus the maximum distance is 4 meters, as only two passengers have thrown up at this point.

Sample Input 2:

There is a single down section and a single passenger, who is not allowed to throw up. One solution would be to start the ride with a speed of 0 m/s, so that it passes the first section with a speed of 5 m/s before reaching the end of the ride and stopping. Thus the maximum distance is 1 meter.