Beau's Route

Beau loves climbing mountains. Specifically, they love the view from the top, which is why when they climb two mountains that are right next to each other, they are usually disappointed after the second one, since the view is basically the same as the first one. In fact, when Beau climbs any mountain, Beau's enjoyment of that mountain is equal to how far away it is from the last mountain they climbed. Auckland has $N$ mountains. All $N$ mountains are laid out in a row with equal spacing between them. They are numbered 1 to $N$, left to right. Beau would like to climb all $N$ mountains in some order, and they would also like to minimise their disappointment. As such, Beau has asked you to write a program that produces a route for them. A route is a sequence in which Beau can climb all of the mountains, where they only climb each mountain once. All Beau asks, is that the least enjoyment they will experience on any mountain on the route is as high as possible. Beau will always enjoy the first mountain they climb greatly, because they haven't climbed any mountains before it.

All of this is to say, Beau would like you to find the route that maximises their minimum enjoyment of every mountain after the first.

Input

Input consists of a single integer $N$, the number of mountains.

Output

Output one line, containing $N$ space separated integers, the $i$th of which should denote the $i$th mountain Beau should climb. You should output every integer $1$ through $N$ exactly once. In other words, your route should be a permutation of the integers $1$ through $N$.

If there are multiple routes that all equally maximise Beau's minimum enjoyment of any mountain except the first, output the one of lowest lexicographical value†.

Constraints

• $2 ≤ N ≤ 100,000$

Subtasks

• Subtask 1 (20%): $N$ is even
• Subtask 2 (40%): $N ≤ 8$
• Subtask 3 (40%): No further constraints

Sample Explanation

There are 4 mountains. Beau should start by climbing mountain 2, then mountain 4. These are two spaces apart, so Beau will have an enjoyment of 2. After that, Beau should climb mountain 1. Mountain 1 is 3 spaces from mountain 4, so Beau will have an enjoyment of 3. Finally, Beau should travel 2 spaces to mountain 3 for an enjoyment of 2. Beau enjoyed mountains 4 and 3 the least, with an enjoyment of 2. This is the largest possible. The path 3 -> 1 -> 4 -> 2 also achieves a minimum enjoyment of 2, but it is lexicographically greater than the one achieved by starting at mountain 2.

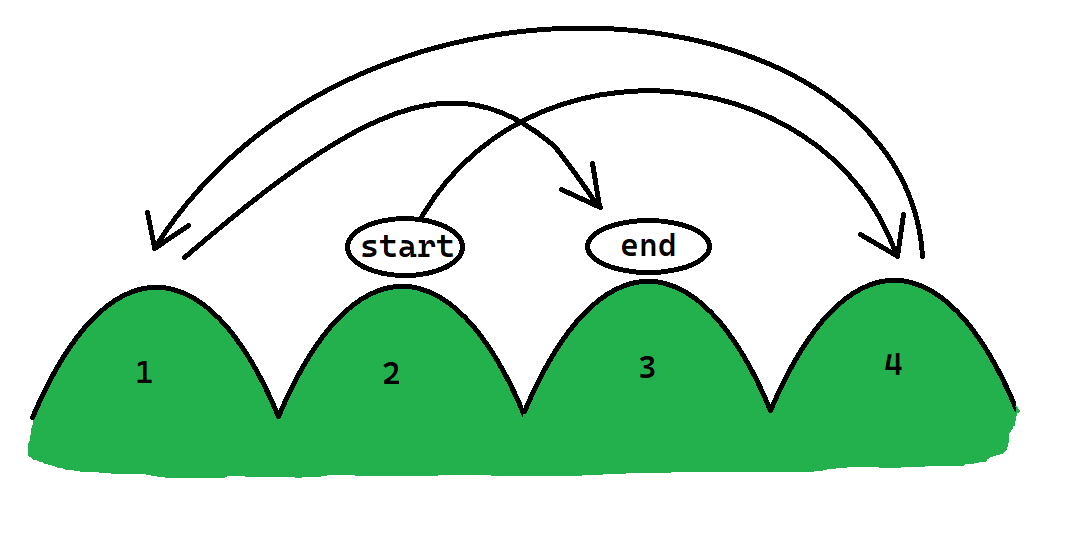
†This is to say that between two routes that equally satisfy Beau's requirement, Beau would prefer the one with the smaller first mountain. If two or more routes have the same first mountain, Beau would like the one with the smaller second mountain, and so on.