Iván's Adventure

Iván has recently been on a long trip around the world - visiting many places such as Hollywood, Lisbon and Fuji.

As we all know, the world is a plane in which $N$ cities are located, numbered from 0 to $N-1$. The $i^\text{th}$ city is located at coordinates ($x_i$, $y_i$). The distance between two cities is measured in a straight line. Thus, the distance between two cities $a$ and $b$ is $\sqrt{(x_a - x_b)^2 + (y_a - y_b)^2}$.

If Iván is in some city $a$, he can go to any other city $b$ by taking a flight. The cost of such a flight, in dollars, is simply the distance between these two cities, rounded up.

Iván's journey can be described as a series of $M$ stops ($s_0, s_1, \cdots, s_{M-1}$) which are not necessarily unique. Simply, he started in city number $s_0$, then took a flight to city $s_1$, then took a flight to city $s_2$ and so on, until he reached city $s_{M-1}$ where he was left with no money.

At every stop on his journey, Iván wonders what cities he can reach. Specifically, for each stop, he wants to know the number of cities he can reach using the money he has left, using some series of flights. Note that this count doesn't include the city he is currently in.

Write a program to help Iván find this out.

Input

The first line of input will contain the two integers $N$ and $M$, separated by a space.

Following this will be $N$ lines, each describing the location of a city. Specifically, the $i^\text{th}$ of these lines will contain the two integers $x_i$ and $y_i$ separated by a space.

Finally, on the last line there will be $M$ space separated integers representing Iván's stops. The $i^\text{th}$ of these integers is $s_i$.

Output

Output a single line with $M$ space-separated integers, the $i^\text{th}$ integer should be the number of cities Iván could reach from his $i^\text{th}$ stop.

Constraints

For all subtasks:

• $2 \le N,M \le 10^5$
• $0 \le x_i, y_i \le 10^7$ for all $i$
• $0 \le s_i < N$ for all $i$
• The positions of all cities are unique.
• Any two consecutive stops are different.

Subtasks

Additional constraints may apply to subtasks:

• Subtask 1 (10%): $N, M \le 50$
• Subtask 2 (15%): $N, M \le 500$
• Subtask 3 (20%): $y_i = 0$ for all $i$
• Subtask 4 (25%): $x_i, y_i \le 500$ for all $i$
• Subtask 5 (30%): No further constraints

Sample Explanation

The path and position of the cities in the first sample sample are shown below.

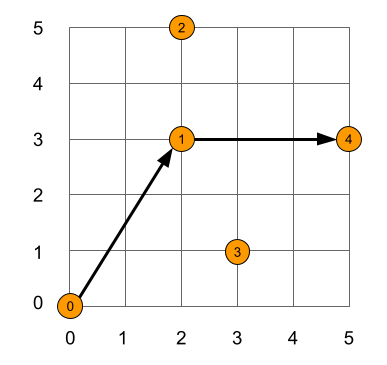
At his first stop, city 0, we can figure out that Iván has $7 and can reach all the other cities using some series of flights.

• He could reach city 1 with a $4 flight
• He could reach city 2 with a $6 flight. If he wanted, he could also reach it by first flying to city 1 ($4), then flying to city 2 ($2), also totalling $6.
• He could reach city 3 with a $4 flight. He could also reach it by flying through city 1.
• He could reach city 4 with a $6 flight. He could also reach it by flying through city 1.

At his second stop, city 1, Iván is left with only $3. This is enough for him to reach all cities except city 0.

At his third stop, city 4, Iván has used all his money and so cannot reach any cities.

Note

• If you are using Python, select Python 3.6 (PyPy 7.3) when submitting. Otherwise, your solution may not pass the time limit even if it is maximally efficient.
• If you're using a type-sensitive language such as C, C++, C# or Java, you should use double precision floating-point types to prevent floating-point error. Namely, you should use double instead of float.