Mischievous Gnomes

You are going on a hike to go and pick apples from The Grand Tree. The Grand Tree is unfortunately located within the Forest of Gnomes. In this forest there are $N$ clearings numbered $0$ through $N - 1$ which are connected by a series of $M$ bidirectional trails. Each trail connects some clearing $a_i$ to clearing $b_i$ and has a length of $c_i$ kilometres. It is guaranteed that there is some series of trails connecting any two clearings, and any pair of clearings will be connected by at most one trail. You start your hike in clearing $0$ and wish to get to The Grand Tree which is located in clearing $N - 1$.

Within the Forest of Gnomes, there live $G$ groups of mischievous gnomes numbered $0$ through $G - 1$. The $i$-th group of mischievous gnomes has a home in clearing $h_i$, and no two groups will share a home clearing. Gnomes are rather small and the groups have varying levels of fitness, so group $i$ can only cause mischief in their home clearing and any clearing that is at most $r_i$ kilometres away.

Any clearing where you could possibly encounter a group of mischievous gnomes is known as an annoying clearing. For your hike from clearing $0$ to The Grand Tree you want to figure out the minimum number of annoying clearings that you need to walk through (including clearing $0$ and $N - 1$), and the length of the shortest path that walks through the minimum number of annoying clearings.

Input

The first line contains, $N, M, G$ separated by spaces. The number of clearings, the number of trails, and the number of groups of gnomes.

The following $M$ lines contain $a_i, b_i, c_i$ separated by spaces, which indicate that clearing $a_i$ and $b_i$ are connected by a trail of length $c_i$.

The next $G$ lines contain $h_i$ and $r_i$ separated by spaces, which indicate that there is a group of gnomes who live in clearing $h_i$ and could be encountered in any clearing within $r_i$ kilometres.

Output

On the first line output the minimum number of annoying clearings that you need to walk through to reach The Grand Tree from clearing $0$.

On the second line output the length of the shortest path that goes through the minimum number of annoying clearings.

Constraints

• $2 \le N \le 100,000$
• $M \le 100,000$ and for $0 \le i < M$:
  • $0 \le a_i, b_i < N$ and $a_i \ne b_i$
  • $1 \le c_i \le 10,000$
• $0 \le G \le N$ and for $0 \le i < G$:
  • $0 \le h_i < N$
  • $0 \le r_i \le 10^9$

Subtasks

• Subtask 1 (17%): $N \le 1,000$, $M = N - 1$, and $a_i = i$ and $b_i = i + 1$ for all $0 \le i < M$, that is, the clearings are arranged in a row from clearing $0$ to clearing $N - 1$.
• Subtask 2 (24%): $G = 0$, there are no gnomes.
• Subtask 3 (23%): $r_i = 0$, that is, every groups of gnomes is lazy and cannot leave their home clearing.
• Subtask 4 (36%): No further constraints.

Notes

If you are using Python and your solution is exceeding the time limit, try selecting Python 3.11 (PyPy 7.3.19) when submitting as this will generally make your code run faster.

Sample Explanation

Sample 1

The minimum number of annoying clearings that you need to walk through to reach clearing $4$ from clearing $0$ is $2$ and the shortest possible path that walks through $2$ annoying clearings is $9$km long. This sample would be valid input for Subtask 1 and Subtask 4.

Sample 2

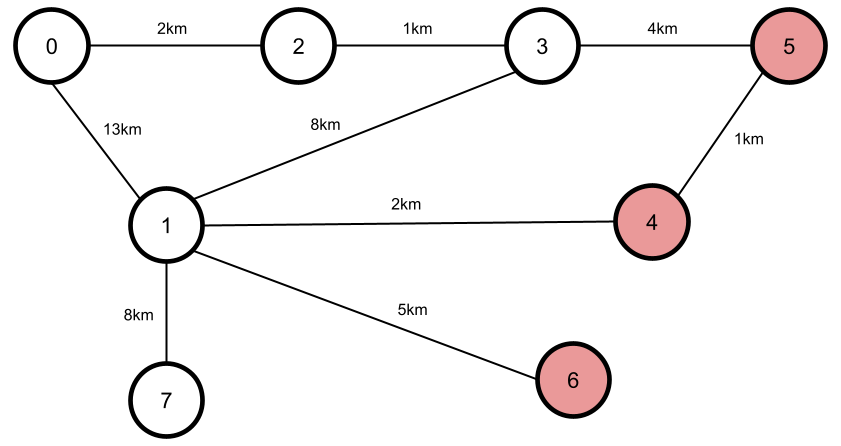
You can walk from clearing $0$ to clearing $7$ without walking through any annoying clearings. The shortest path in which you do not walk through any annoying clearings is $0 \rightarrow 2 \rightarrow 3 \rightarrow 1 \rightarrow 7$ which has a length of $19$km. This subtask would be valid input for Subtask 4.