Perimeters

Alison is in year 7 and she love Maths, in particular Measurement. She figures that to work out the perimeter of a rectangle she doesn't need the lengths of all sides to be given to her. If the rectangle is drawn on a plane (fancy word alert: Cartesian plane) and the sides of the rectangle are parallel to the x and y axes, then she can figure the perimeter if she is given the bottom left vertex (unfancy word: corner) coordinates and the top right vertex coordinates.

Input

The first line of input contains 2 integers, $A$ and $B$, the x and y coordinates of the bottom left hand vertex.

The second line of input contains 2 integers, $C$ and $D$, the x and y coordinates of the top right hand vertex.

Output

Print a single integer - the distance on the Cartesian plane that is the perimeter of the rectangle.

Subtasks

For all test cases, $A < C$ and $B < D$. The following subtasks are available:

• Subtask 1 ($50\%$): $A, B, C, D > 0$
• Subtask 2 ($50\%$): $-1000 \leq A, B, C, D \leq 1000$

Sample Data Explanation

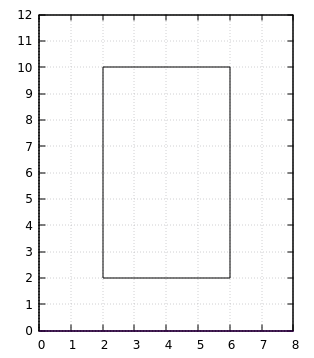
The diagram above corresponds to the sample data. The length of the horizontal line is the difference between the x values: $6 - 2 = 4$. The length of the vertical line is the difference between the y values: $10 - 2 = 8$. The perimeter is the sum of the four sides: $4 + 4 + 8 + 8 = 24$